How to solve the "nic" problem
This is a good brain teaser for mathematicians to waste time with.
810
STEPS
TOOLS
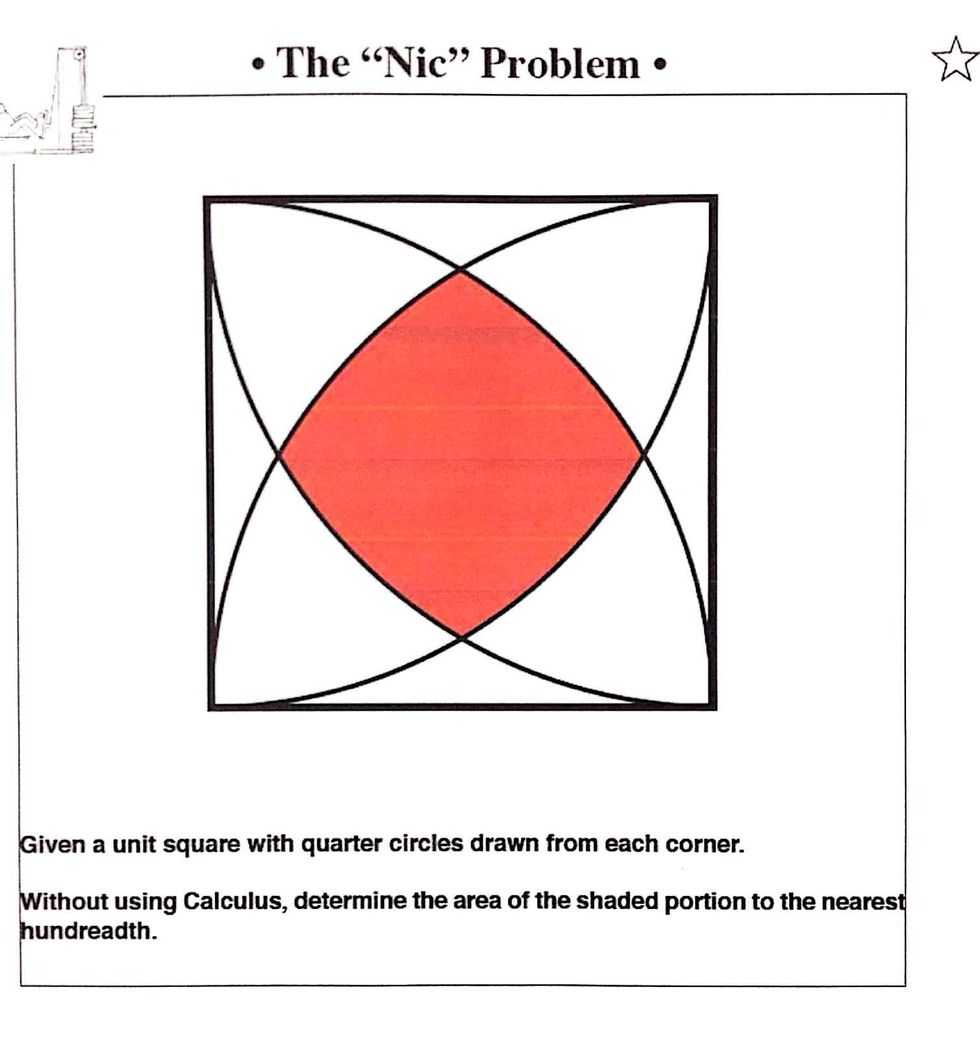
So you want to solve for the shaded region inside the unit circle with quarter circles drawn from corner to corner. But the directions doesn't want us to use Calculus, so we won't.
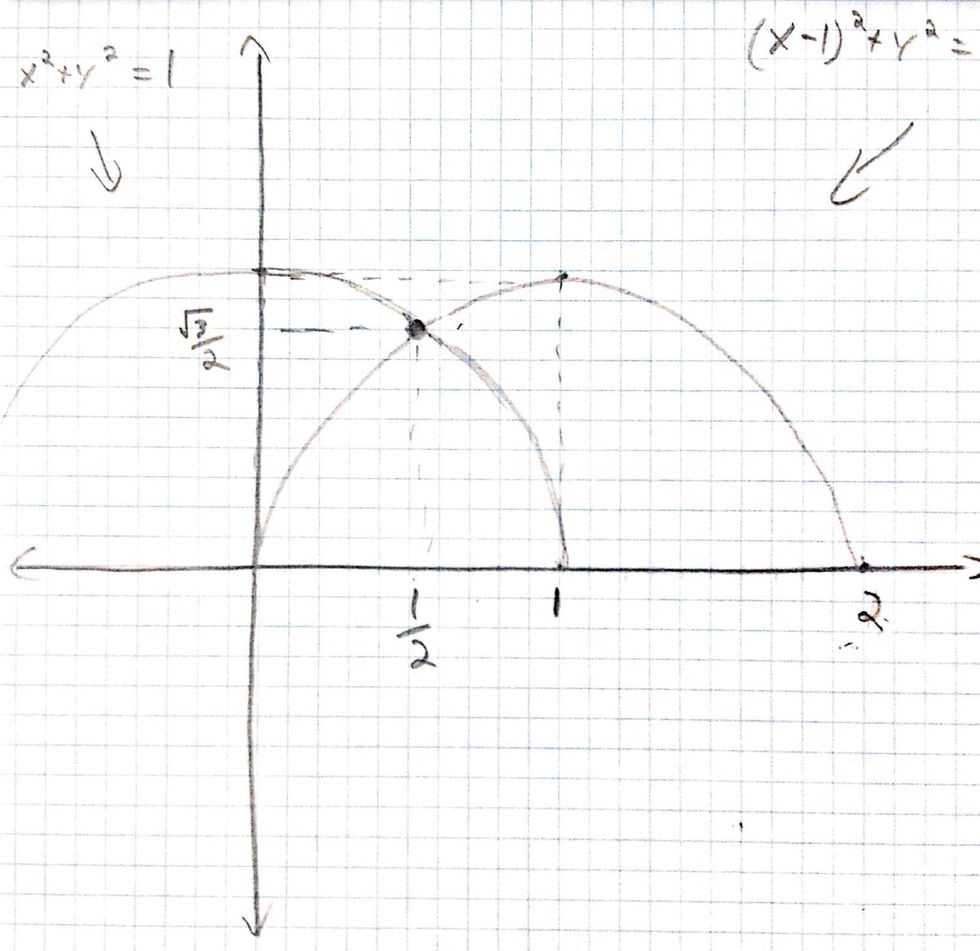
First, let's graph half of a unit circle and another half of a unit circle shifted 1 unit to the right. Find the point where they intersect. Note the height of the intersection. It's about .866.
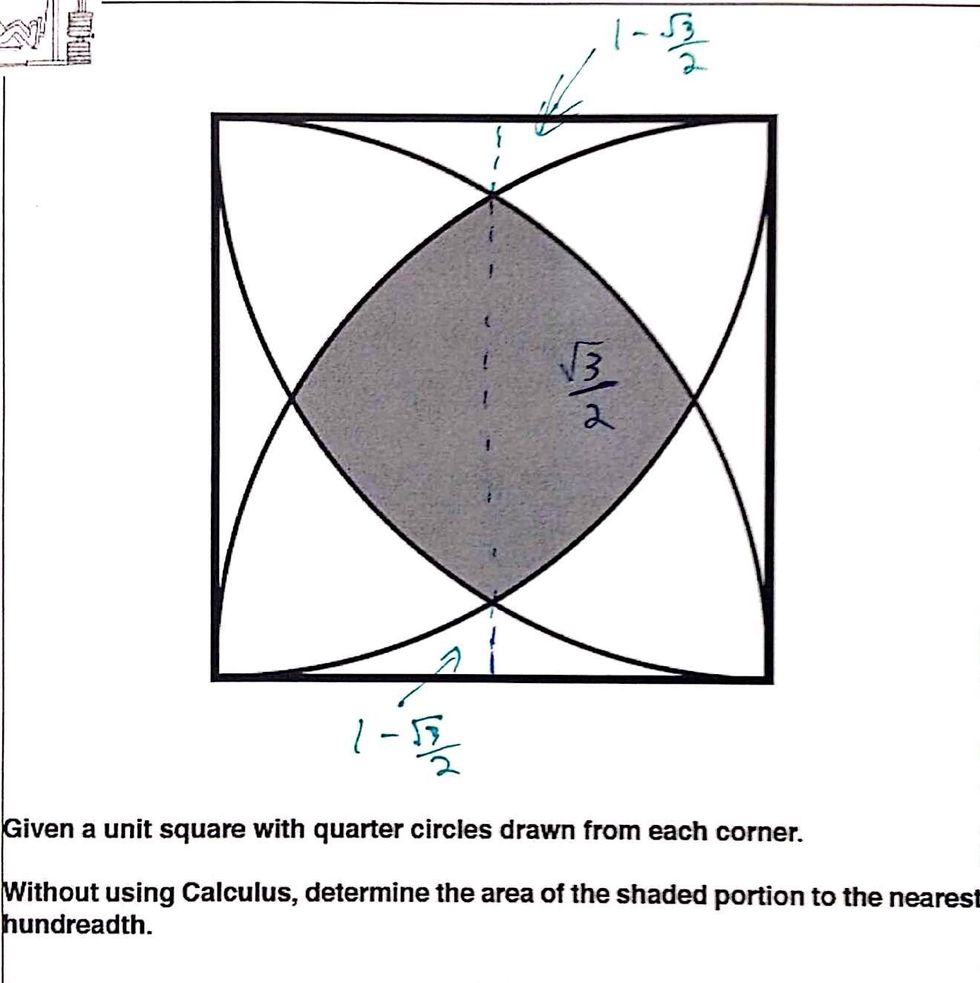
Now that we know the length from the top of the intersection to the bottom of the square is .866, we can figure out the the length of the cross length in the shaded region. It's about .732
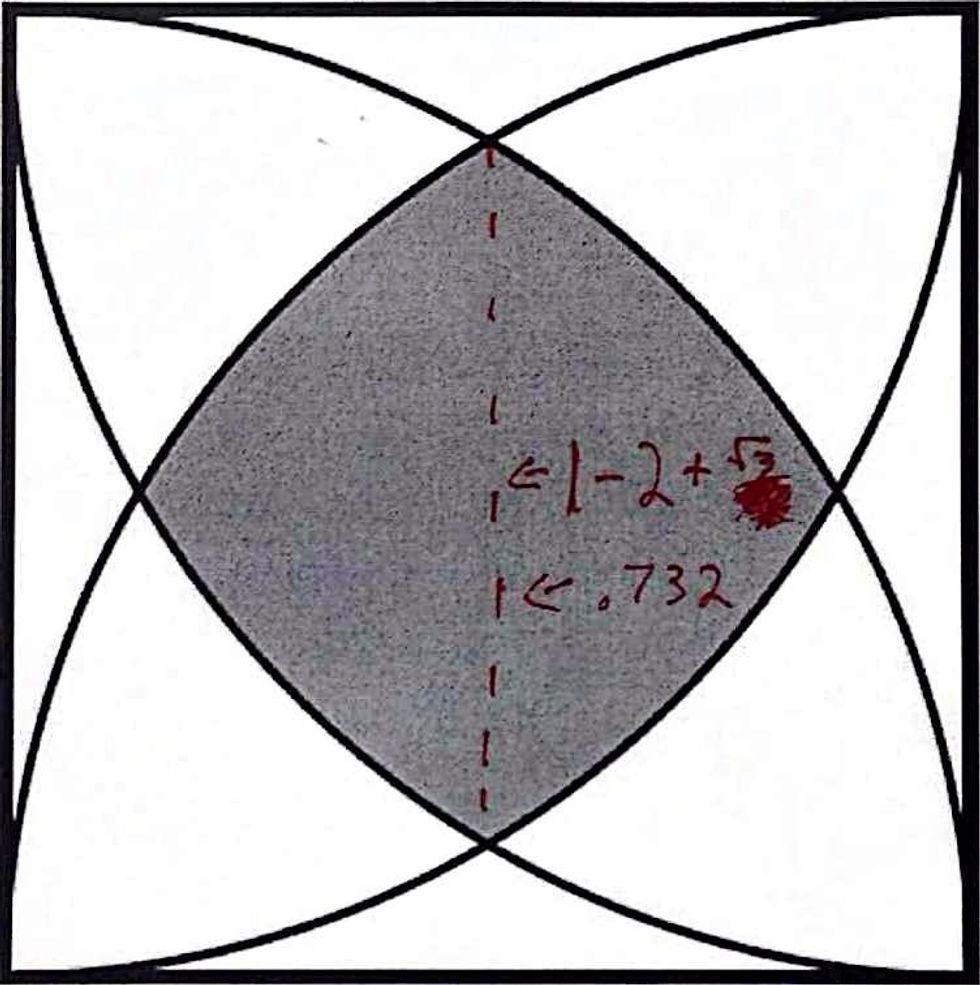
Yep .732.
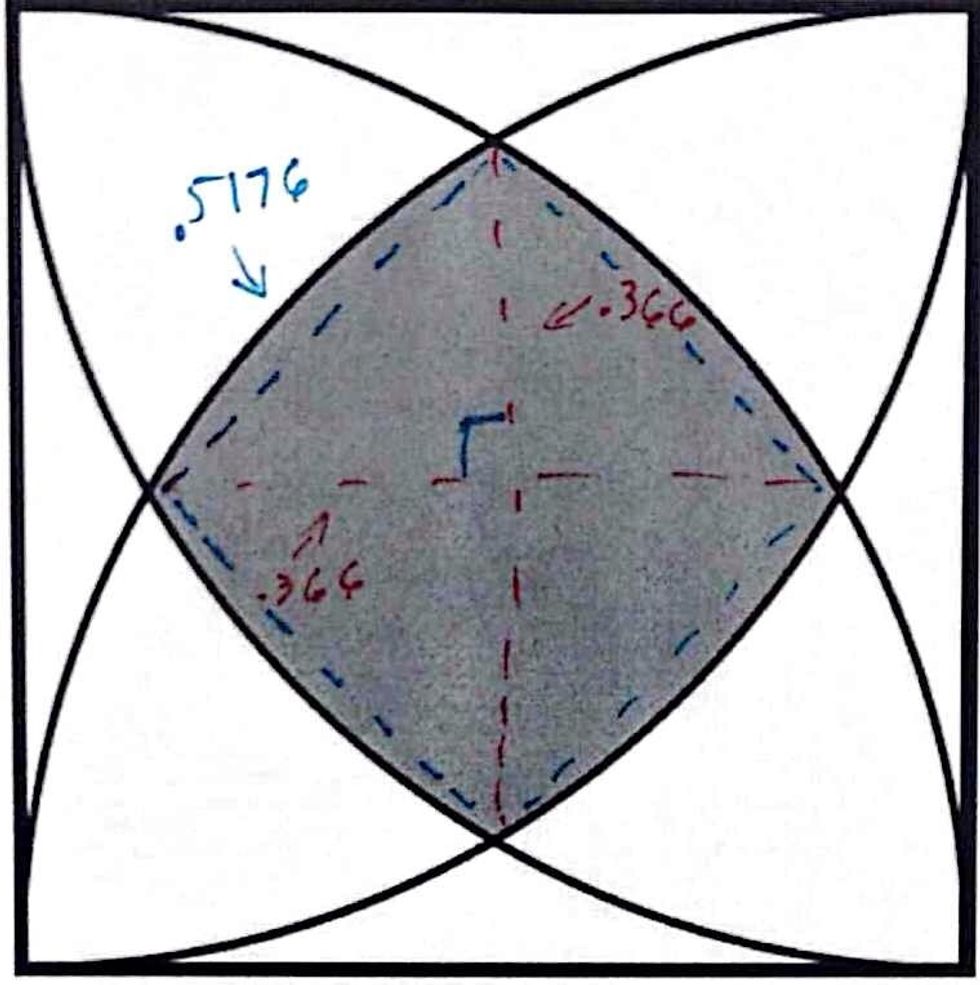
If we draw lines to each endpoint, make a square and 4 right triangles. The next step is find the sides of the square using pathagoryan theorem. The sides of the square is about .5176.

Now you want to make a isosceles triangle using a side of the square as a base. You want to find the area of this triangle and subtract it from pi/12 to find the area of the bulge out of the square.
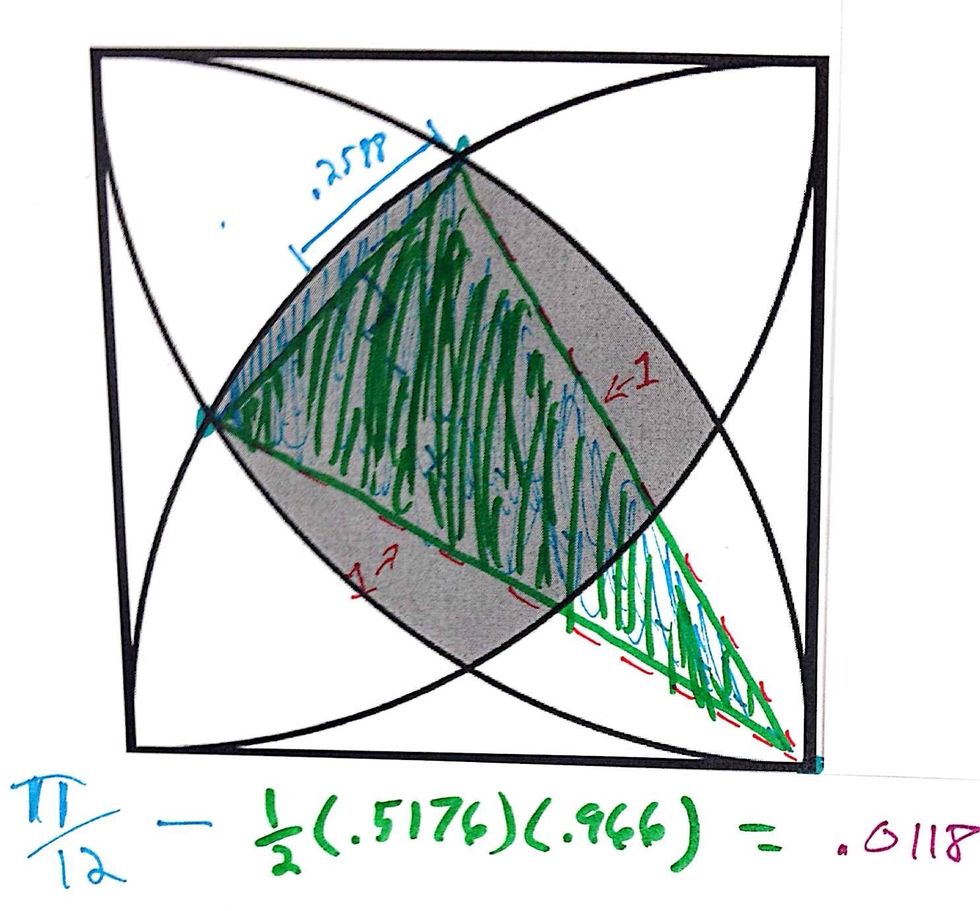
The area of a unit circle is pi (3.15). A quarter of that is pi/4. Notice that we cut the the quarter circle in 3 equal pieces. So dividing pi/4 by 3 give us pi/12. So, pi/12 - .5(.5176)(.966) = .0118

So add the area of the 4 bulges and the area of the square together and you should get .3151, which rounded to the hundredth place is .32!
This took me a while to figure out. Even I couldn't figure it out all by myself, partly do to silly mistakes. But in the end its pretty easy. My coworker had another way to solve but I like this way.
There are more ways to solve it too. That's what makes math great! Go to your local Mathnasium and get a mental work out!
The creator of this guide has not included tools
The Conversation (0)
Sign Up