How to solve partial fractions by decomposition.

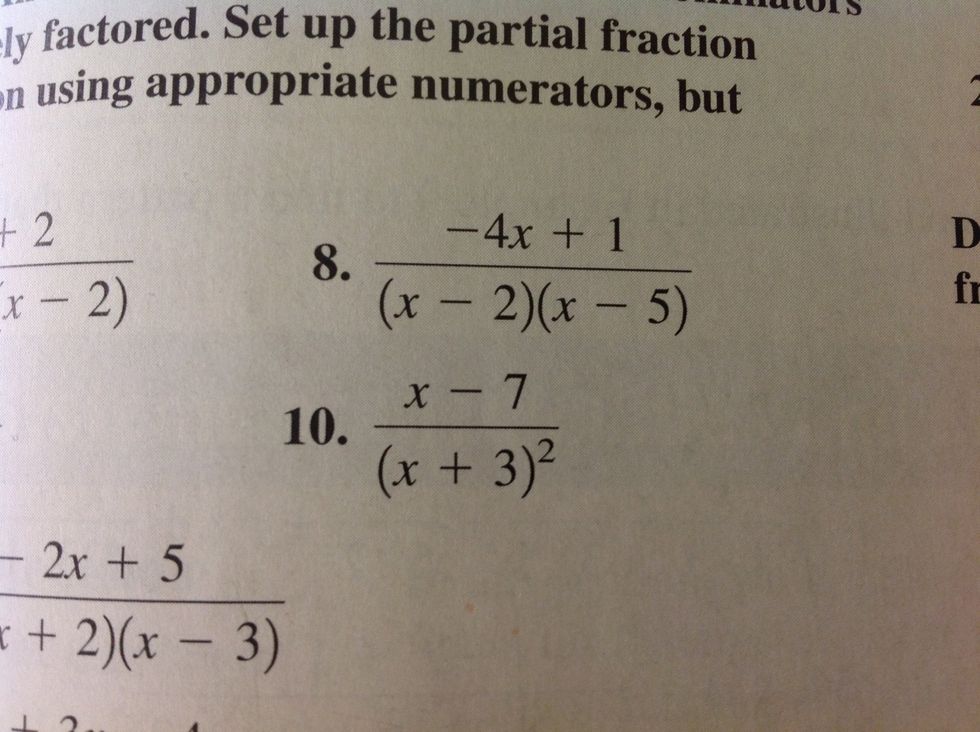
Let's solve number eight. We first make sure that the denominator has a higher degree than the numerator, which defines a partial fraction.

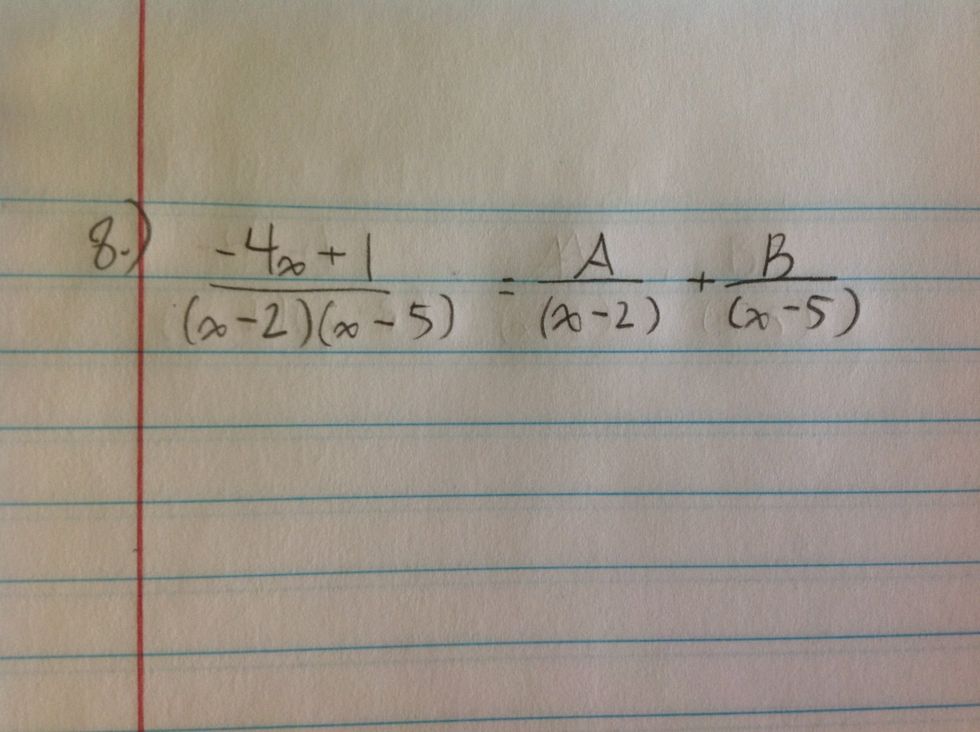
Since the denominator is already factored out, we can set the fraction into the appropriate template. The numerator is not quadratic, so we use A and B only.

Next, we multiply everything by the least common denominator, which is (x-2)(x-5) in this case...

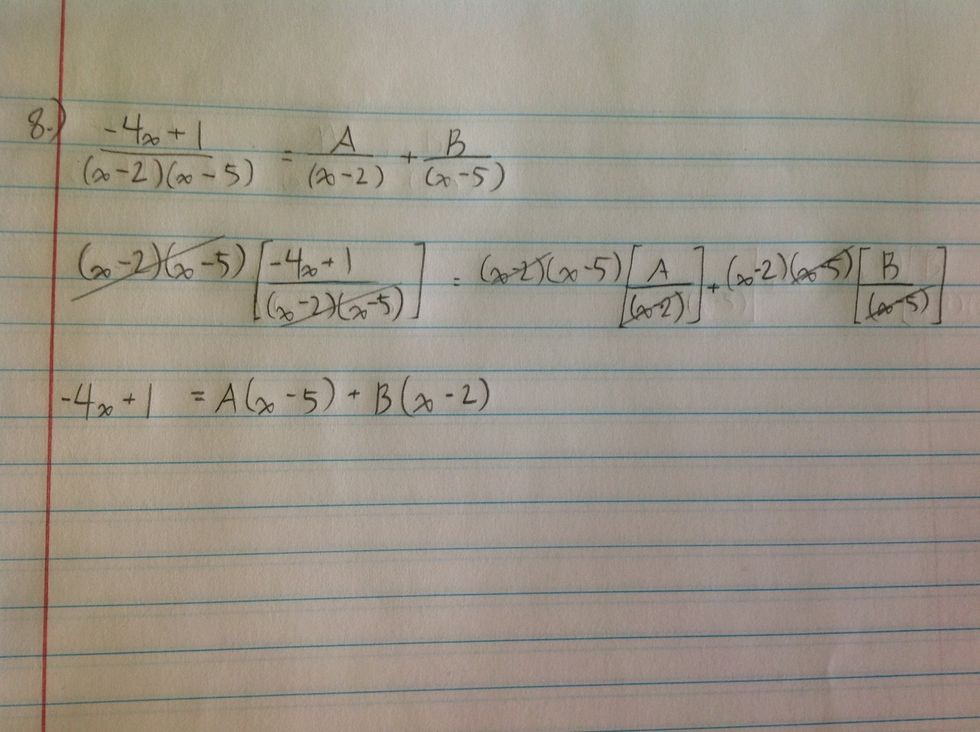
... So all the denominators cancel out and the fractions simplify.

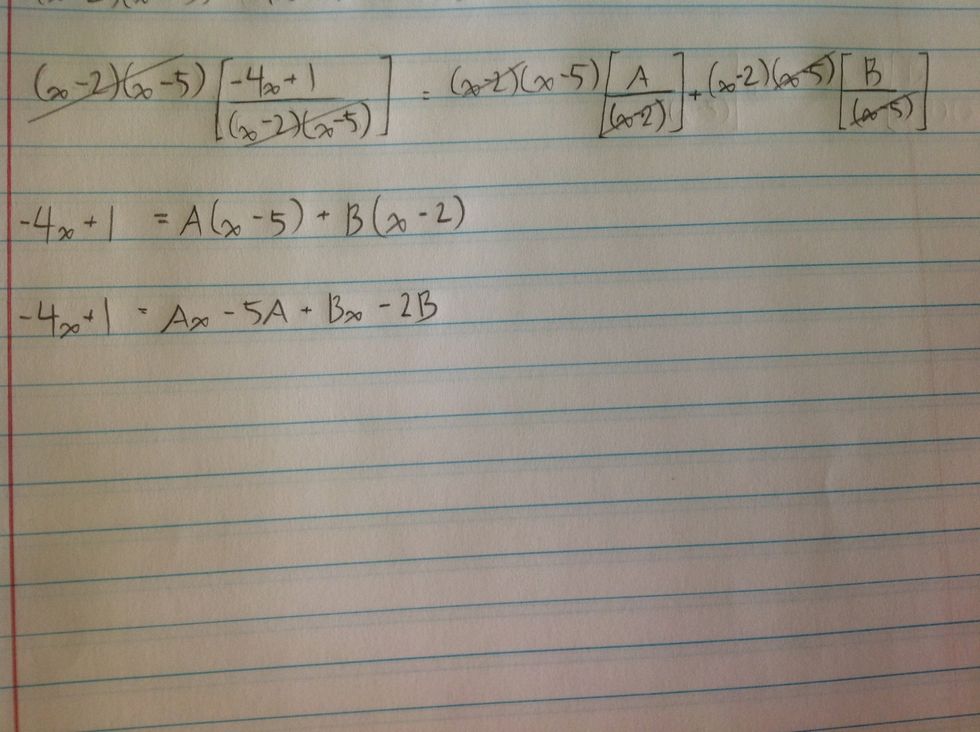
Multiply the variables out.

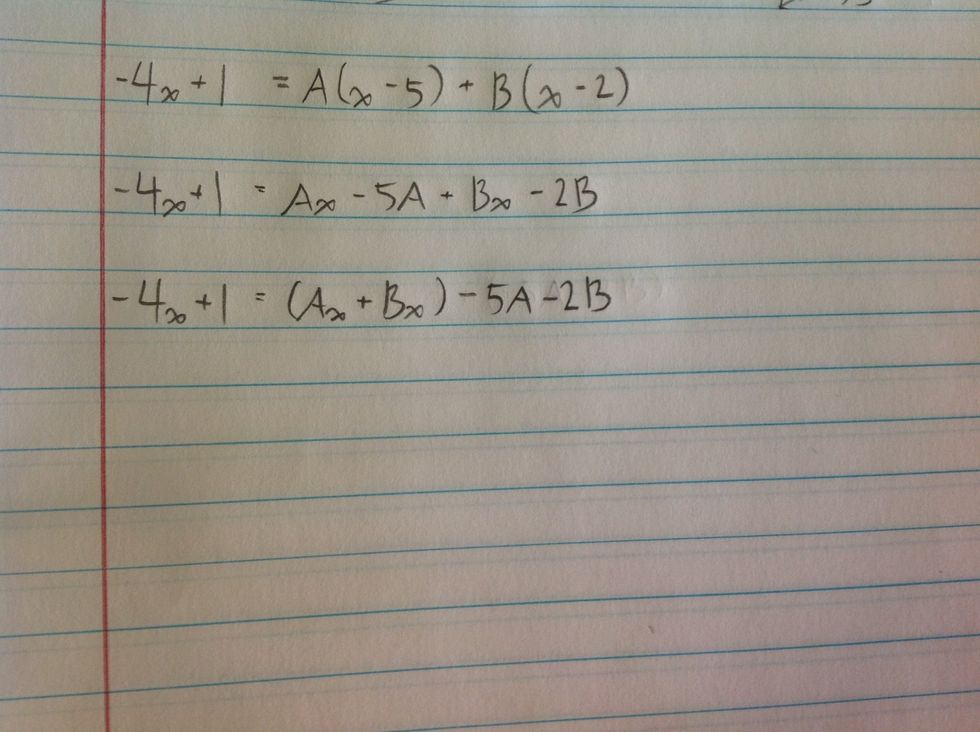
Group like terms.

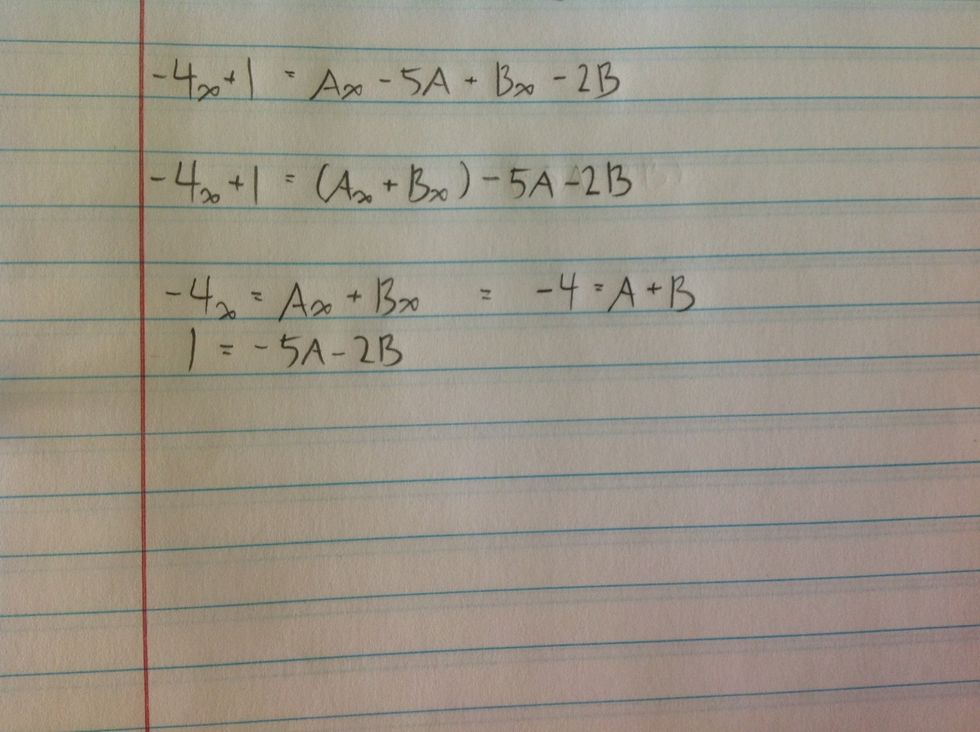
Set each group of terms equal to the appropriate number and simplify.

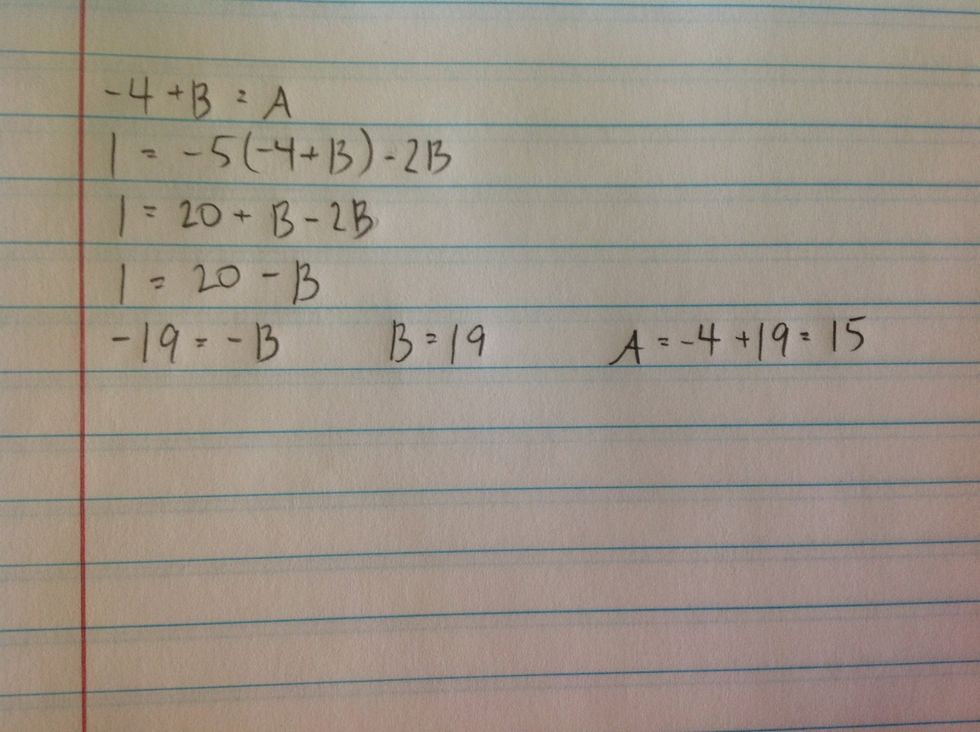
Solve for each variable, and we find that A equals 15 and B equals 19. However, we are not finished yet!

The last step is to plug the numbers back into the original template, and we are done!

Math is POWER!